毕设工作即将结束之际,附上一份笔记到博客-数学物理方程-热传导方程.
反问题与不适定问题
反问题描述
note quote 一对问题称为是互逆的
不适定问题的三个判断标准
- 问题的解是存在的;
- 问题的解是唯一的;
- 问题的解是稳定的;
该概念由现法国科学院院士 J.Hadamard 在耶鲁大学提出. 适定(well-posed)问题 & 不适定(ill-posed)问题.
$$ Ax=y, A: X \rightarrow Y 的线性紧算子 $$
1、解的存在性:$ \forall y \in Y, \exist x \in X, $ 使得 $ Ax=y. $
2、解的唯一性:$ \forall y_1, y_2 \in Y, y_1 \neq y_2, $ 有 $ Ax_1=y_1, Ax_2=y_2, $ 使得 $ x_1 \neq x_2. $
3、解的稳定性(即解的连续性):若有 $ Ax_1=y_1, Ax_2=y_2, $ 则当 $ y_1 \rightarrow y_2 $ 时, 使得 $ x_1 \rightarrow x_2. $
note info 当定解条件(初值条件,边界条件)以及方程中的系数有微小变动时,相应的解也只有微小变动. 解的稳定性也称为解关于参数的连续依赖性.
微分方程
微分方程:包含导数的方程,常用于描述现实事物的变化. 微积分学是一门研究变化的学问. 微分应用包括对速度、加速度、曲线斜率、最优化等的计算.
- 微分方程的定解条件:即初值条件和边界条件;
- 三类边界条件
- 第一类:狄利克雷边界条件(Dirichlet boundary condition)也被称为常微分方程或偏微分方程的“第一类边界条件”,指定微分方程的解在边界处的值. 求出这样的方程的解的问题被称为狄利克雷问题.
- 第二类:诺伊曼边界条件(Neumann boundary condition) 也被称为常微分方程或偏微分方程的“第二类边界条件”. 诺伊曼边界条件指定了微分方程的解在边界处的微分.
- 第三类:Robbin条件/混合边界条件,未知函数在边界上的函数值和外法向导数的线性组合.
- 偏微分方程三大问题
- 初边值问题或混合问题:偏微分方程 + 初值条件 + 边界条件;
- 初值问题或 Cauchy 问题:偏微分方程 + 初值条件;
- 边值问题:偏微分方程 + 边界条件;
- 方程式与方程组
- 方程式:方程个数为 1;
- 方程组:方程个数大于 1;
- 欠定与超定
- 欠定:方程个数少于未知函数个数;
- 超定:方程个数多于未知函数个数;
- 方程(组)中出现的未知函数的最高阶偏导数的阶数称为方程(组)的阶数.
数学物理微分方程反问题的分类
文献[1]根据以下一般形式的微分方程组,给出了数学物理反问题的五大分类.
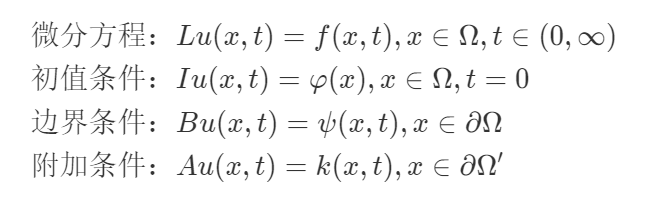
其中 $ u(x,t) $ 为微分方程组的解;$ L, I, B, A $ 分别是微分算子,初始算子,边界算子和附加算子. $ \Omega $ 为求解区域,$ \partial \Omega $ 为求解区域的边界. $ \partial \Omega^{\prime} $ 为 $ \Omega $ 的一部分. $ f(x,t) $ 为方程的右端项,$ \varphi(x), \psi(x,t), k(x,t) $ 分别为初始条件、边界条件和附加条件. 上述任一已量变为未知量,即为微分方程反问题.
- 参数识别问题:算子 $ L $ 未知(通常 $ L $ 的结构是已知的,未知的为算子中的参数);
- 寻源反问题:右端方程源项 $ f(x,t) $ 未知;
- 逆时反问题:$ \varphi(x) $ 条件未知时,附加条件为系统某一时刻的状态,该反问题从后面的状态去确定初始状态;
- 边界控制问题:边界条件 $ \psi(x,t) $ 未知;
- 几何反问题:区域边界 $ \partial \Omega $ 未知;
反问题通常是不适定的,即初始条件上的一个微小的扰动,将导致结果的巨大变化. 克服反问题不适定性是比较棘手的,这也是反问题研究的重要课题.
随机微分方程解的爆破:在大多数时间里,解是有解的。但存在某一时间点,解趋于 $ \infty $.
任何一个物理现象都是处在特定条件下的.
关于反问题的更多描述
关于反问题的一个比较适用的数学定义是“由定解问题的解的部分信息去求定解问题中的未知成分”. 有效反问题的数值算法以正问题的高精度解法为基础.
反问题的不适定性主要表现在两个方面: 一方面,由于客观条件限制的输入数据(即给定的解的部分已知信息)往往是欠定的或者是超定的,这就导致解的不唯一性或者是解的不存在性; 另一方面,反问题的解对输入数据往往不具有连续依赖性。由于输入数据中不可避免的测量误差,人们就必须提出由扰动数据求反问题在一定意义下近似解的稳定的方法. 因此,反问题和不适定问题是紧密联系在一起的.
定解条件都是通过测量和统计而得到的,在测量和统计的过程中误差总是难免的,同时在建立数学模型的过程中也多次用了近似. 如果解的稳定性不成立,那么所建立的定解问题就失去了实际意义. 如果一个定解问题的适定性不成立,就要对定解问题作进一步地修改,直到它具有适定性[3].
热传导方程
Direct heat conduction problems (DHCPs) 直接热传导问题, Inverse heat conduction problem (IHCPs) 逆热传导问题
热传导正/反问题
- 热传导反问题:在热交换情形下,通过研究物体内部或边界的一点或多点温度分布信息来反演热源项、初始条件、边界条件、物理的几何条件等未知量.
- 热传导方程非特征 Cauchy 问题的[4]:典型的热传导方程的非特征Cauchy问题是通过一部分边界上的或者内部的数据来判定另一部分边界的热流.
一维热传导方程初边值问题
有限域上边界条件为第一类 Dirichlet 边界条件的数学模型:
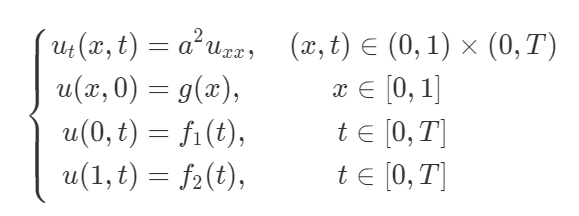
求解区域:
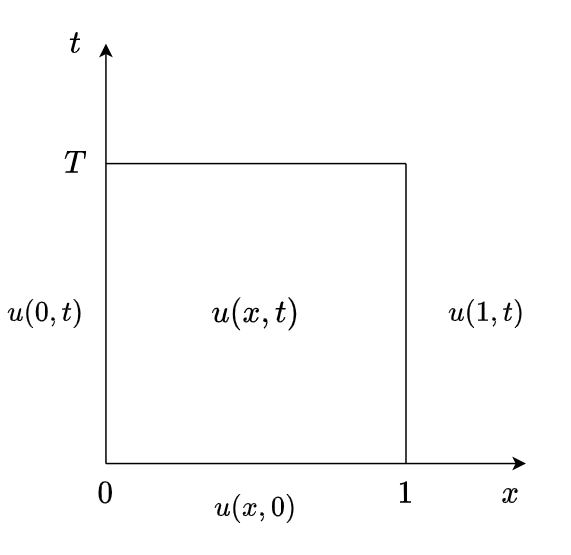
处理热传导方程非特征 Cauchy 问题的相关方法
基本解方法
基本解方法(the method of fundamental solutions, MFS)使用微分算子的基本解去近似数值解.
热传导方程非特征 Cauchy 问题使用基本解方求解时,数值近似解由以下基本解的线性组合得到[5]:
$$
\begin{array}{c}
\tilde{u}(x) = \sum_{i = 1}^{N} a_{i} u^{*}\left(x-\mu_{i}\right)
\end{array}
$$
待定系数 $ a_{i} $ 通过对求解区域边界和虚边界进行配置点配置得到. 基本解方法是一种无网格的径向基函数类方法.
因 Cauchy 问题的不适定性,基本解方法所得到的线性系统是高度病态的,常规方法求解已没有意义. 需要使用正则化方法处理线性系统的病态性.
正则化方法
正则化方法求解不适定问题的本质是, 对问题的解进行一定的限制, 考虑一个近似的适定问题来保证原问题近似解的稳定性.
- Tikhonov 正则化方法
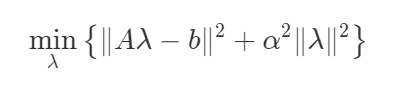
正则化参数 $ \alpha $ 的选取.
- 确定式方法
- 偏差原则
- 拟最优方法
- 启发式方法
- 广义交叉核式
- L-曲线法则
参考
- [1] 张智倍. 热传导方程反问题的若干方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.
- [2] 臧顺全. 热传导方程正问题和反问题的数值解研究[D]. 西安: 西安理工大学, 2019.
- [3] 王明新. 数学物理方程[M]. 清华大学出版社, 2005: 1-171.
- [4] 贾现正. 热传导方程中的若干反问题[D]. 上海: 复旦大学, 2005.
- [5] 金邦梯. 一类椭圆型偏微分方程反问题的无网格方法[D]. 杭州: 浙江大学, 2005.