二分查找算法

二分查找的基本思想: 将 n 个元素分成大致相等的两部分，取 a[n/2] 与 x(查找目标值) 做比较，如果x == a[n/2] ,则找到 x,算法中止；否则，如果x < a[n/2],则只要在数组 a 的左半部分继续搜索 x,如果x > a[n/2], 则只要在数组 a 的右半部搜索 x。

使用二分查找算法的前提：待查找序列是有序的

时间复杂度分析

由算法核心思想可知：每次对比都将下一步的比对范围缩小一半。每次比对后剩余数据项如下表:

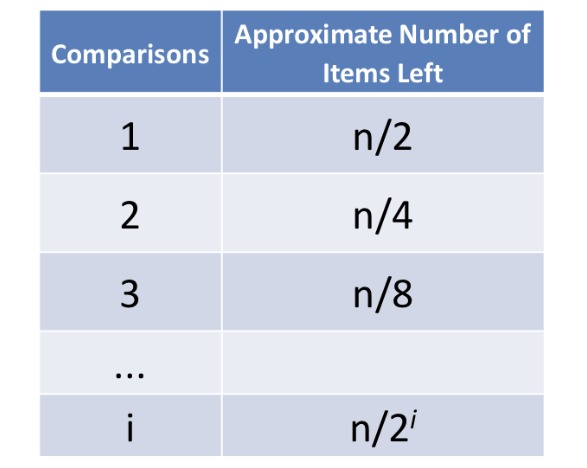
最好情况

即要找的元素正好在初始查找序列的中间一次比较出结果，时间复杂度为 $ O(1) $。

最坏情况

即比对范围只剩下 1 个数据项的情况这个数据项即为正要找的元素。这时，可求解如下方程组($ i $ 为比较次数)：

$$ \frac{n}{2^i}=1 $$

时间复杂度为 $ O(log(n)) $

平均时间复杂度

进行平均时间复杂度分析时需要讨论：随着元素个数n的增多，需要几步算法才能终止？查找成功有多少种情况？查找失败有多少种情况？

设 $ n=2^k-1 $, $ k $ 为比较次数。易知，对于 $$ t=1,2,…, \lfloor log(n) \rfloor + 1 $$, 会有 $ 2^{t-1} $ 个元素在 $ t $ 步之后使算法成功终止。总共有 $ (2n+1) $ 种情况，$ n $ 种情况为成功结束，$ (n+1) $ 种情况为失败终止。

由此可得二分搜索的平均比较次数为 $ (k = \lfloor log(n) \rfloor + 1) $：
$$ A(n)= \frac{1}{2n+1}(\sum_{i=1}^{k}i2^{i-1} + k(n+1)) $$
根据初等数学等差乘等比数列求和的错位相减法/裂项相消法。易知,
$$ \sum_{i=1}^{k}i2^{i-1} = 2^k(k-1)+1 $$

使用裂项相消法
由 $ \sum_{i=1}^{k}i2^{i-1} $，设 $ a_i=i2^{i-1},(i=1,…,k) $。注意到，$ a_i=(k-1)2^k-(k-2)2^{k-1} $。
$$ \sum_{i=1}^{k}i2^{i-1}=0\times2^1+1+1\times2^2-0\times2^1+2\times2^3-1\times2^2+…+(k-1)2^k-(k-2)2^{k-1}=2^k(k-1)+1 $$

$$ A(n)= \frac{1}{2n+1}(\sum_{i=1}^{k}i2^{i-1} + k(n+1)) $$
$$ \sum_{i=1}^{k}i2^{i-1} = 2^k(k-1)+1 $$
综上可得，$$ A(n) = \frac{1}{2n+1}((k-1)2^{k}+1+k2^k) $$

当 $ n $ 非常大时，可得
$$ A(n) \approx \frac{1}{2^{k+1}}((k-1)2^{k}+k2^k)=\frac{(k-1)}{2}+\frac{k}{2}=k-\frac{1}{2} $$
所以 $ A(n)<k=O(log(n)) $ ，平均时间复杂度为$ O(log(n)) $。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# -*- coding: utf-8 -*-
# binary_search

def binary_search(list_1, item):

    low = 0
    high = len(list_1)-1

    while low <= high:
        '''使用 // 整除运算符可以不用int进行类型转换'''
        #每次都检查中间的元素
        mid = (low + high)/2
        guess = list_1[int(mid)]

        if guess == item:
            return int(mid)#返回所在位置的索引
        if guess < item:   #猜的数字小了，修改low
            low = mid+1
        if guess > item:   #猜的数字大了，修改high
            high = mid-1
    return None

def main():

    list_2 = [1,2,3,4,5,6,7,8,9]

    print(binary_search(list_2, 8))
    print(binary_search(list_2, 10))

main()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

#include<iostream>
#include<typeinfo>
using namespace std;

int binary_search(int a[9],int n,int x)//n为元素个数
{
    int mid;
    int high,low=0;
	int guess;

    high = n-1;//数组下标从0开始

	while(low <= high)
    {
        mid = (high+low)/2;
        guess = a[mid];
        if(guess == x)
            return mid;
        if(guess > x)
            high = mid-1;
		if(guess < x)
		    low = mid+1;
    }
    return -1;
}

int main()
{
	int temp;
    int a[9] = {1,2,3,4,5,6,7,8,9};

	cout<<sizeof(a)/sizeof(int)<<endl;
	cout<<typeid(sizeof(a)/sizeof(int)).name()<<endl;
    temp = binary_search(a,sizeof(a)/sizeof(int),5);
	cout<<temp<<endl;

	return 0;
}

附：C++ 使用头文件typeinfo下的typeid(parameter).name()可获取参数获取类型名