有限状态机(Finite State Machine)
有限状态机(英语:finite-state machine,缩写:FSM)又称有限状态自动机(英语:finite-state automaton,缩写:FSA),简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学计算模型。- 维基百科
有限状态机的要素
状态:状态是有限个的,任一时刻,只处于一种状态
条件:用于触发状态转移动作的“事件”,条件被满足(输入)就会触发相应动作
动作:条件满足后,执行状态转移的行为
转换:从一个状态转换为另一个状态,转换一般由状态转换函数完成
让我们来看下有限状态机的经典例子:旋转闸机(这年代闸机基本不用硬币了😂)
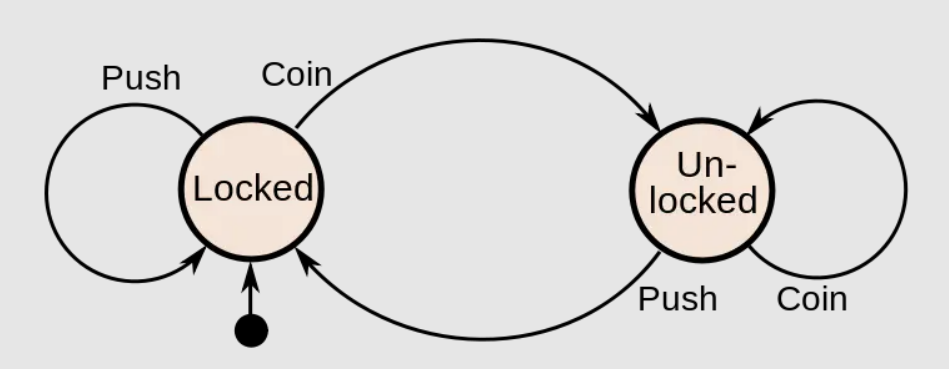
使用状态图表示的话就是下面这样子:
状态:旋转闸机只有两种状态:锁定和解锁
条件、动作、转换:闸机的初始状态 是锁定(Locked)的,当游客放置硬币(Coin)到闸机中时,闸机就会转换为解锁(Un-locked)状态,当游客执行推动作通过闸机后,闸机状态又会被转换为锁定(Locked)。
当闸机处于解锁(Un-locked)状态时,反复的放硬币是没有用的,状态不会变,同理,锁定态时,反复 Push 旋转门也是没用的,闸机状态不会变,游客通过不了。
用状态转换表表示如下图:
Go 实现旋转门的 FSM 基于 Go 语言,可实现旋转门闸机的 FSM 如下,StateTransitionTable 即为状态转换表:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 package mainimport ( "bufio" "fmt" "log" "os" "strings" ) const ( Locked = iota Unlocked ) const ( InputCoin = "coin" InputPush = "push" ) type State uint32 type StateTransitionTableDef struct { State State Input string } type TransitionFunc func (state *State) var StateTransitionTable = map [StateTransitionTableDef]TransitionFunc{ {Locked, InputCoin}: func (state *State) fmt.Println("Unlocks the turnstile so that the customer can push through." ) *state = Unlocked }, {Locked, InputPush}: func (state *State) fmt.Println("The turnstile has been locked." ) }, {Unlocked, InputCoin}: func (state *State) fmt.Println("The turnstile has been unlocked." ) }, {Unlocked, InputPush}: func (state *State) fmt.Println("When the customer has pushed through, locks the turnstile." ) *state = Locked }, } type TurnStile struct { State State } func (t *TurnStile) string ) { stateActionTupple := StateTransitionTableDef{ t.State, strings.TrimSpace(action), } if transFunc := StateTransitionTable[stateActionTupple]; transFunc == nil { fmt.Println("Unknown action, please try again!" ) } else { transFunc(&t.State) } } func main () turnstileFSM := &TurnStile{ State: Locked, } prompt(turnstileFSM.State) reader := bufio.NewReader(os.Stdin) for { action, err := reader.ReadString('\n' ) if err != nil { log.Fatalln(err) } turnstileFSM.ExecuteAction(action) } } func prompt (s State) m := map [State]string { Locked: "Locked" , Unlocked: "Unlocked" , } fmt.Printf("current state is: [%s], please input action: [coin | push]: \n" , m[s]) }
FSM 应用-词法分析 FSM 很典型的一个应用就是用于编译器前端->词法分析器(Lexer)的词法分析上(tokenize)。比如如下关系表达式语句的 tokenize 上:
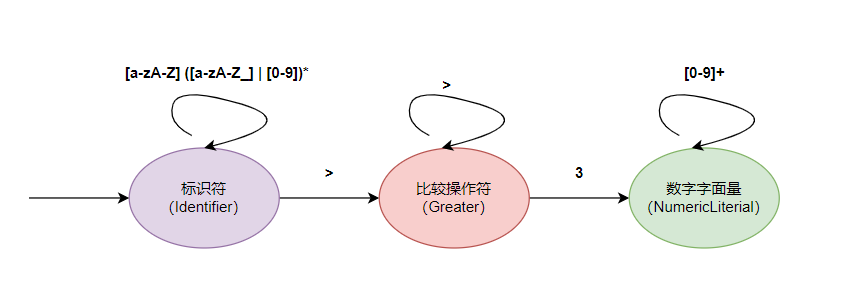
我们的 Lexer 扫描关系表达式时需要识别到 blogAge 为标识符(Identifier),> 为比较操作符(Greater),3 为数字字面量(NumericLiteral),对应的词法规则如下:
标识符(Identifier):首字符需要为字母,其他字符可为数字或字母或下划线
比较操作符(Greater):>
数字字面量(NumericLiteral):全部由数字组成
对应的 FSM 简化版状态图如下:
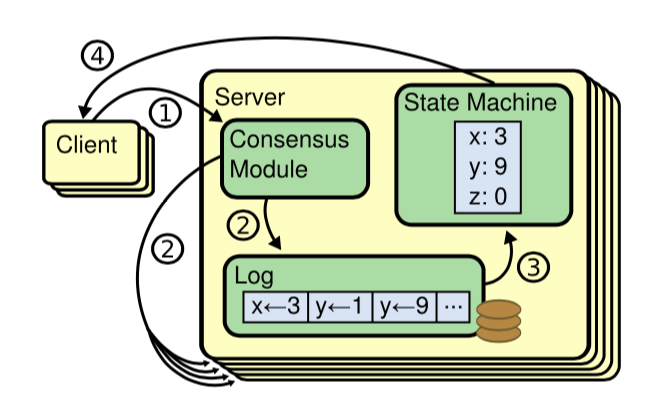
复制状态机(Replicated State Machine) 在分布式系统领域,状态机被用于保证节点状态的一致性,分布式系统一致性算法是基于复制状态机(Replicated State Machine)提出来的。
每一个 Server 节点都会有一个状态机,这个状态机的输入来源为一份储存着命令序列的日志,对于相同的命令输入,每个节点状态机(确定有限自动机 DFA,Deterministic Finite Automata)的输出是确定的、相同的。
参考