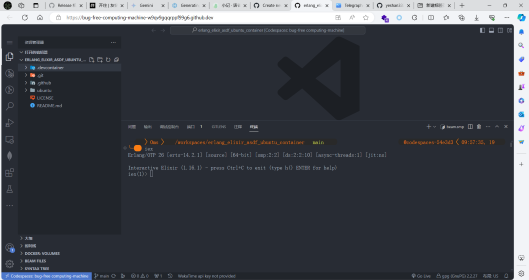
使用 chezmoi & vscode, 管理你的 dotfiles
Awesome Technology Weekly Zh-Hans - 中文技术月/周/日刊一览
Awesome Technology Weekly Zh-Hans - 中文技术月/周/日刊一览, 文章每三小时刷新
乐理通识
2023 年搞了台雅马哈 61 键的电子琴,顺手看了下啊 B 的上的课程 《零基础自学音乐学乐理合集-第一季》,这里是部分笔记(给博客加点不一样的东西👀)。
简谱各部分一览
C 表示音名
竖线为小节线
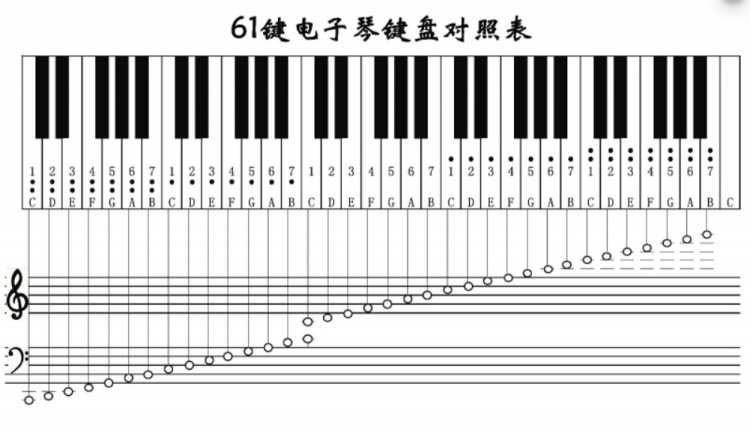
音名
完整钢琴键盘 88 键
9个组,一组 7 个白键,5 个黑键位
键位表示,音名对应的键位
1=C 的意思即简谱中 1 对应的键位,代表 1 从哪个键出发,1 的位置一...
(译) Server-Sent Events: the alternative to WebSockets you should be using
原文地址: https://germano.dev/sse-websockets/作者: Germano Gabbianelli
当开发实时 web 应用时,WebSockets 可能是我们首先想到的。然而,Server Sent Events (SSE) 是通常会是一种更简单的替代方案。
1. 序言最近我对实现实时 Web 应用程序的一些最佳方式很感兴趣。也就是一个应用程序包含一个或多...
2022 | Summary
迟来的总结,2022 五味杂陈,最后的几个月,基本都在尝试着解决某些情绪,这一年有很多东西应该被记录。坚持是最反人性的一种东西,但长远来看,这应该也是最浪漫的东西。这一年,我真正感受到了什么叫信念的崩塌,原来没有了光是这种感觉。或许真正明白了一个道理:没有经历过,只是看过别人的经历,没有多大用的,路走过了才勉强懂了。
博客 & 技术-Blog & Techs看了眼归档 arc...