稳定的直接插入排序

基本思想:
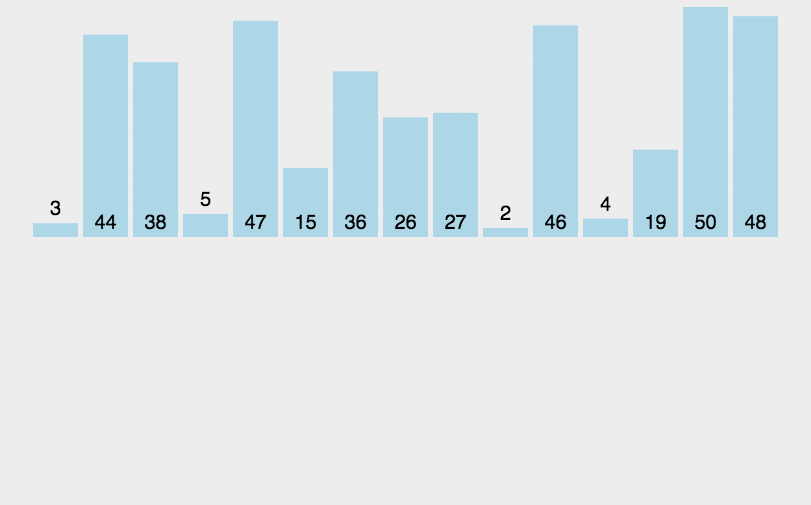
我们将一个待排序序列分为有序区和无序区（一般开始的时候将第一个元素作为有序区，剩下的元素作为无序区），每次将无序区的第一个元素作为待插入记录，按大小插入到前面已经排好的有序区中的适当位置，直到记录全部插入完成为止。(如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面)

二分查找算法 二分查找的基本思想: 将 n 个元素分成大致相等的两部分，取 a[n/2] 与 x(查找目标值) 做比较，如果x == a[n/2] ,则找到 x,算法中止；否则，如果x < a[n/2],则只要在数组 a 的左半部分继续搜索 x,如果x > a[n/2], 则只要在数组 a 的右半部搜索 x。 使用二分查找算法的前提：待查找序列是有序的 时间复杂度分析...

A+B for Input-Output Practice(using C++)

1.

Problem Description
Your task is to Calculate a + b. Too easy?! Of course! I specially designed the problem for acm beginners. You must have found that some problems have the same titles with this one, yes, all these problems were designed for the same aim
Input
The input will consist of a series of pairs of integers a and b, separated by a space, one pair of integers per line.
Output
For each pair of input integers a and b you should output the sum of a and b in one line, and with one line of output for each line in input.
Sample Input
1 6 1 20
Sample Output
7 21